1. 简单线性回归
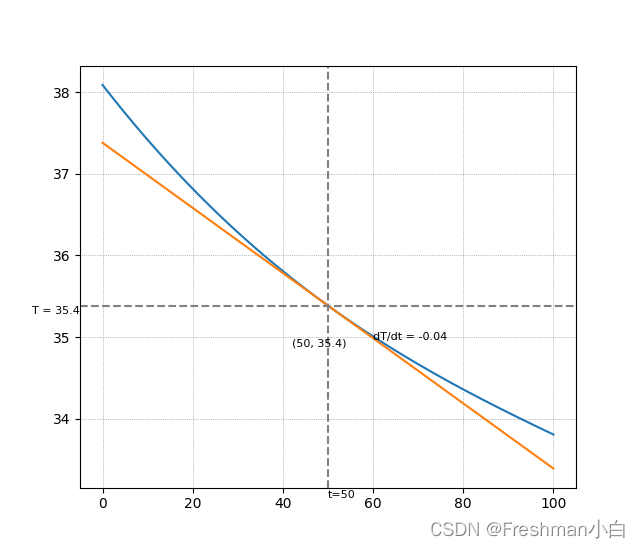
使用回归分析绘制拟合曲线是一种常见的方法,简单线性回归就是其中的一种。简单线性回归可以通过最小二乘法来计算回归系数。以下是一个使用简单线性回归来拟合数据的代码示例:
import numpy as np import matplotlib.pyplot as plt x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) y = np.array([2.5, 4.5, 4.8, 5.5, 6.0, 7.0, 7.8, 8.0, 9.0, 9.5]) # 计算回归系数 slope, intercept = np.polyfit(x, y, 1) # 绘制拟合曲线 plt.scatter(x, y) plt.plot(x, slope * x + intercept, color='red') plt.show()
在该代码中,np.polyfit函数可以用来计算简单线性回归的回归系数。plot函数用来绘制拟合曲线,scatter函数绘制原始数据点。

2. 多项式回归
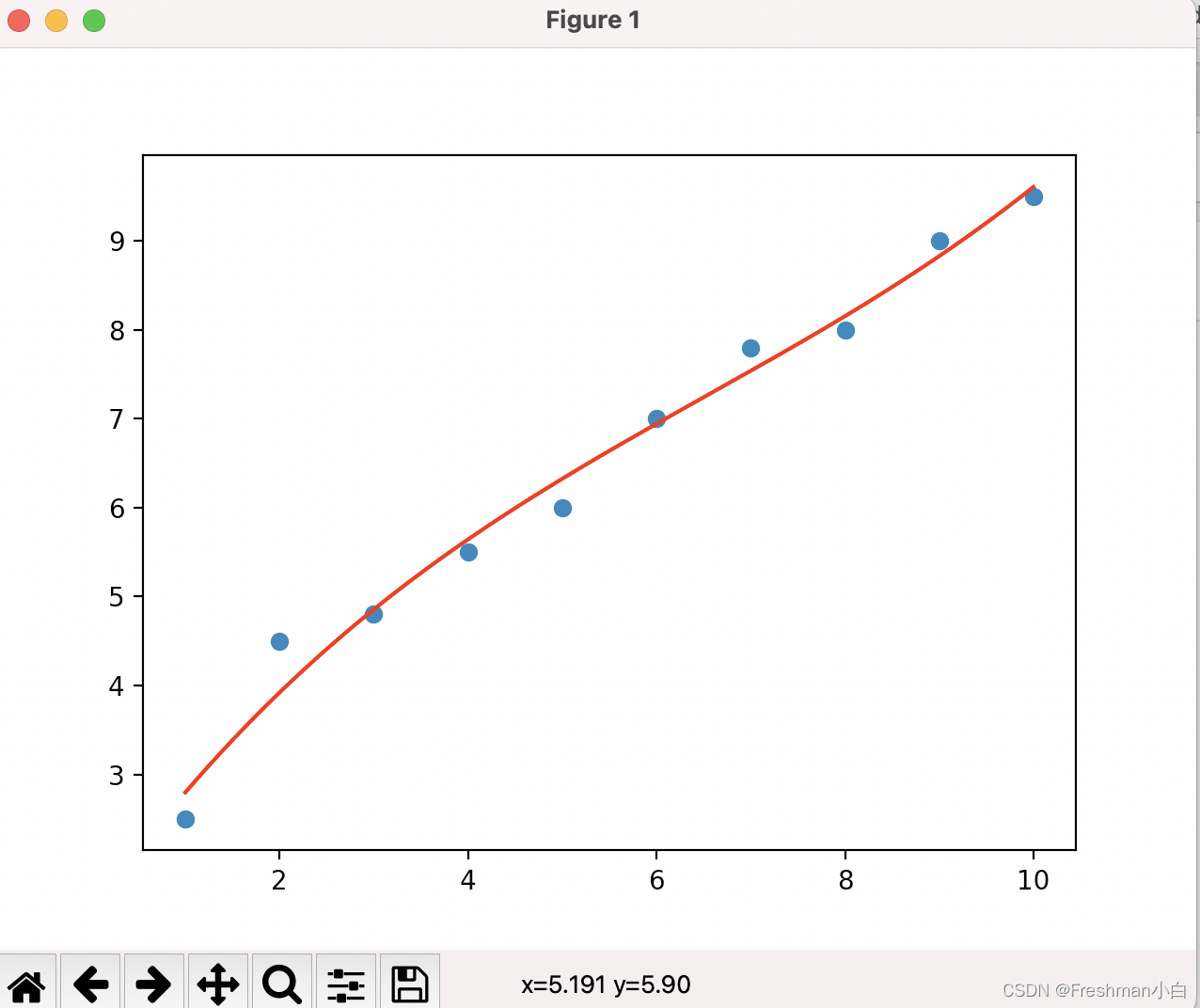
使用多项式回归是一种常用方法,它可以用来拟合更加复杂的数据集。以下是一个使用多项式回归来拟合数据的代码示例:
import numpy as np import matplotlib.pyplot as plt x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) y = np.array([2.5, 4.5, 4.8, 5.5, 6.0, 7.0, 7.8, 8.0, 9.0, 9.5]) # 计算多项式回归系数 coefs = np.polyfit(x, y, 3) # 使用np.poly1d函数来生成一个多项式拟合对象 poly = np.poly1d(coefs) # 生成新的横坐标,使得拟合曲线更加平滑 new_x = np.linspace(min(x), max(x), 1000) # 绘制拟合曲线 plt.scatter(x, y) plt.plot(new_x, poly(new_x), color='red') plt.show()
与简单线性回归不同,多项式回归可以拟合更加复杂的数据集。在该代码中,np.polyfit函数计算多项式回归系数,np.poly1d函数生成一个多项式拟合对象。plot函数用来绘制拟合曲线,scatter函数绘制原始数据点。
3. 非线性回归
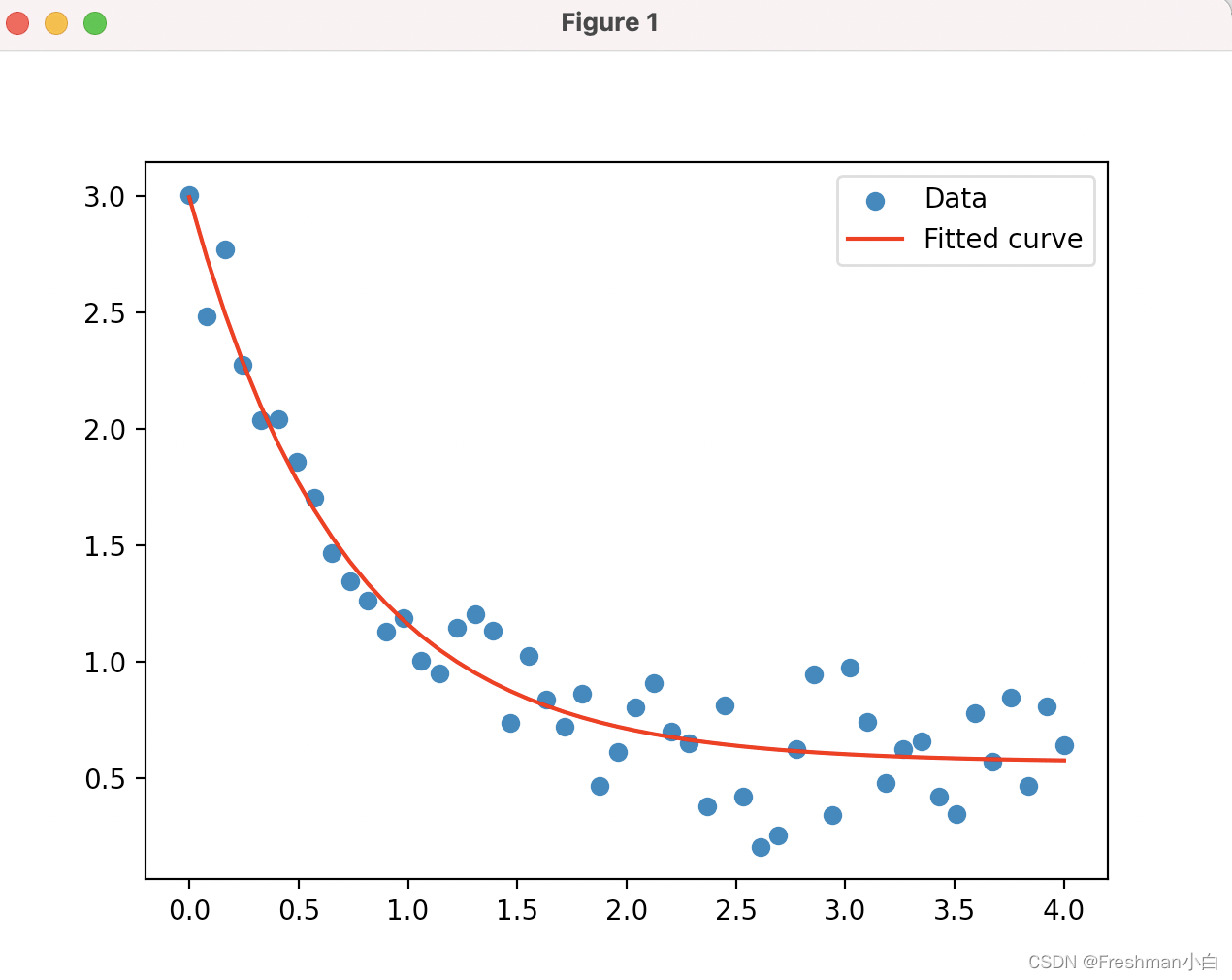
使用非线性回归是一种更加复杂的拟合方法,在实际应用中可以用来拟合更加复杂的非线性数据。以下是一个使用非线性回归来拟合数据的代码示例:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def func(x, a, b, c):
return a * np.exp(-b * x) + c
# 生成模拟数据
x_data = np.linspace(0, 4, 50)
y_data = func(x_data, 2.5, 1.3, 0.5) + 0.2 * np.random.normal(size=len(x_data))
# 使用curve_fit函数来拟合非线性数据
popt, pcov = curve_fit(func, x_data, y_data)
# 画出原始数据和拟合曲线
plt.scatter(x_data, y_data, label="Data")
plt.plot(x_data, func(x_data, *popt), color='red', label="Fitted curve")
plt.legend()
plt.show()
在该代码中,使用了Scipy库中的curve_fit函数来拟合非线性数据。curve_fit函数中第一个参数是非线性函数,第二个参数是拟合数据的横坐标,第三个参数是拟合数据的纵坐标。
总结
以上是Python中的三种常用拟合曲线方法。简单线性回归可以拟合线性关系的数据,多项式回归可以拟合更加复杂的数据,而非线性回归则可以用来拟合非线性数据。我们可以根据实际需要选择不同的方法来拟合数据。

